Satu Hektar Sama Dengan Berapa Meter Persegi?

Satu Hektar Sama Dengan Berapa Meter Persegi - Pertanyaan seperti itu seringkali muncul di benak kita. Meskipun sebenarnya materi yang membahas hal tersebut sudah pernah diajarkan dalam pelajaran matematika di sekolah tidak sedikit orang yang lupa mengenai hal tersebut. Oleh sebab itu, Rumus Matematika Dasar tergugah untuk mengangkat materi mengenai hal tersebut. Untuk mengembalikan ingatan anda mengenai materi yang berkaitan dengan satuan hektar, di sini akan disajikan penjelasan sederhana yang dapat membantu anda dalam menentukan berapa meter persegi-kah satu hektar itu?

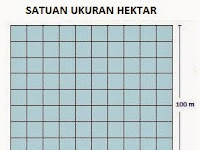
Satuan hektar diambil dari kata "hekto are" dan di dalam matematika biasa dilambangkan dengan ha. Biasanya ukuran ini digunakan untuk menyatakan luas dari sebuah bidang datar berbentuk persegi. Dari gambar di atas kita dapat melihat bahwasannya satu hektar mewakili luas dari persegi yang memiliki sisi sepanjang 100 meter. Artinya, satu hektar sama dengan 100 meter x 100 meter = 10.000 m².

Contoh Soal Perhitungan Luas dalam Satuan Hektar dan Pembahasannya

Untuk memperdalam pemahaman mengenai satuan hektar, tidak ada salahnya apabila kita mempelajari beberapa contoh soal di bawah ini:

Contoh soal 1:

Sebuah lapangan sepakbola memiliki luas 3,7 ha. Berapakah luas dari lapangan tersebut?

Jawab:

Diketahui1 ha(hektar) = 10.000 m2, maka:

3,7 ha = 3,7 x 10.000

3,7 ha = 37.000 m²

Jadi luas lapangan sepakbola tersebut adalah 37.000m²

Contoh soal 2:

Sebidang tanah berbentuk persegi panjang memiliki ukuran panjang 200 m dan lebar 32 m. Berapakah luas tanah tersebut jika dinyatakan dalam satuan hektar?

Jawab:

Luas tanah = 200 m x 32 m

Luas tanah = 6.400 m²

Karena 1 hektar = 10.000 m², maka:

6.400 : 10.000 = 0,64 hektar

Maka, luas tanah tersebut adalah 0,64 ha

Contoh Soal 3:

Sebuah taman memiliki luas 3,43 hektar. Berapakah luas taman tersebut bila dinyatakan dalam are?

Jawab:

Diketahui 1 hektar = 100 are, maka:

3,43 hektare = 3,43 x 100 are = 343 are.

Jadi luas taman tersebut adalah 343 are.

Contoh Soal 4:

Pak Bejo memiliki sawah seluas 4,6 hektar. Berapakah luas sawah pak Bejo bola dinyatakan dalam meter persegi?

Jawab:

Diketahui 1 ha = 10.000 m², maka:

4,6 ha = 4,6 x 10.000 = 46.000m²

Jadi luas sawah yang dimiliki pak andi adalah 46.000m²

Jadi sekarang kita tidak perlu pusing dan bingung lagi ketika pertanyaan Satu Hektar Sama Dengan Berapa Meter Persegi? menghampiri kita. Dari penjelasan di atas kita sudah bisa mengetahui bahwasannya satu hektar itu sama dengan 10.000 meter persegi. Semoga pembahasan ini bermanfaat dan bisa membantu anda yang sedang kebingungan dalam menentukan satuan ukuran hektar (ha).

Contoh Latihan Soal Cerita Aljabar untuk Kelas 7 SMP Semester Ganjil

Contoh Latihan Soal CeritaAljabar untuk Kelas 7 SMP – Tak bosan-bosannya Rumus Matematika Dasarmenghadirkan beragam contoh soal untuk membantu kalian dalam mempersiapkan diri menghadapi ulangan ataupun ujian. Pada postingan kali ini contoh soal yang akan diberikan adalah mengenai aljabar. Sebelumnya juga telah diberikan contoh soal serupa dalam artikel 5 Contoh Soal Cerita Aljabar Matematika . Namun, untuk soal kali ini sedikit berbeda karena bentuk soalnya adalah soal cerita. Soal-soal seperti ini seringkali muncul dalam kategori Essay atau isian singkat di dalam ulangan semester ataupun ujian nasional. 

Tidak ada salahnya bila kalian mencoba kemampuan kalian untuk memecahkan persoalan-persoalan matematika yang ada di bawah ini:

Kumpulan Contoh Latihan Soal Cerita tentang Aljabar untuk SMP Kelas 7

Soal 1

Di dalam tas terdapat 3 buah buku, 2 penggaris, dan 2 pensil. Kemudian Ani memasukkan lagi 2 buah buku dan 1 buah pensil. Tanpa sepengetahuan Ani, adiknya mengambil 1 buah buku, 1 buah pensil, dan 1 buah penggaris. Berapakah jumlah masing-masing alat tulis yang ada di dalam tas Ani?

Soal 2

Pak Badu memelihara 3 ekor Sapi, 5 Ekor itik dan 10 ekor kambing.   Pada suatu hari pak badu membutuhkan uang lalu ia menjual 1 ekor sapi dan 2 ekor ayam di pasar. Beberapa hari kemudian pak Badu membeli lagi 3 ekor itik dan 2 ekor kambing. Berapakah jumlah ternak yang dimiliki pak Badu saat ini?

Soal 3

Di sebuah toko komputer terdapat 10 laptop, 5 komputer dan 3 speaker.  Pada suatu hari ada beberapa barang yang terjual yaitu 3 laptop dan 2 komputer, kemudian toko tersebut mendapat kiriman dari pabrik berupa  2 unti laptop, 2 komputer dan 2 speaker. Berapakah jumlah alat elektronik yang sekarang ada di toko computer tersebut?

Soal 4

Di sebuah toko bunga terdapat 50 tangkai bunga melati, 100 tangkai bunga mawar dan 40 tangkai bunga tulip. Ada seorang pelanggan yang membeli 20 tangkai bunga melati dan 20 tangkai bunga tulip.  Lalu toko bunga tersebut membeli lagi 20 tangkai bunga melati, 20 tangkai bunga mawar dan 40 tangkai bunga tulip. Maka, berapakah jumlah bunga yang ada di toko bunga tersebut?

Soal 5

Pak Hasan membeli  100 sak semen, 1000 buah batu bata dan 120 batang kayu, jumlah material yang sudah digunakan untuk membangun rumah adalah  20 sak semen, 500 batu bata  dan 50 batang kayu, karena material tersebut masih kurang,  akhirnya pak Hasan membelli lagi 40 sak semen, 200 buah batu bata dan 70 batang kayu. Berapakah jumlah bahan bangunan yang ada sekarang?

Soal 6

Di dalam kulkas terdapat 2 tomat, 4 kubis  dan 5 wortel kemudian ibu mengambil 1 tomat, 2 kubis dan 1 wortel. Setelah itu, Ibu membeli lagi 1 tomat, 2 kubis dan 2 wortel. Berapakah  jumlah sayuran yang ada di dalam kulkas sekarang?

Soal 7

Di sebuah tempat parkir ada  3 truk, 5 motor dan 2 mobil, lalu keluarlah 1 truk dan 2 motor. Kemudian ada lagi yang parkir yaitu 2 truk, 1 motor, dan 1 mobil. Lalu, berapakah jumlah masing-masing kendaraan yang ada di tempat parkir tersebut saat ini?

Soal 8

Di sebuah toko furniture ada10 buah kursi, 8 meja dan 6 lemari. Pada suatu hari terjual 2 kursi, 2 meja dan 3 lemari.  Kemudian dating lagi kiriman berupa 3 buah kursi, 2 meja dan 4 lemari. Sekarang ada berapa furniture yang dijual di toko furniture tersebut?

Bagaimana? Mudah atau sulitkah Contoh Latihan Soal Cerita Aljabar untuk Kelas 7 SMP yang diberikan di atas? Semoga kalian semakin mahir dalam menjawab soal-soal dengan bentuk serupa. Sampai berjumpa lagi di dalamcontoh-contoh soal dengan materi yang lainnya.

Sistem Pertidaksamaan Linear Dua Variabel Kelas X SMA

Sistem Pertidaksamaan Linear Dua Variabel - Jika sebelumnya Rumus Matematika Dasar telah memberikan pembahasan materi mengenai sistem persamaan linear dua variabel, untuk melengkapi materi pelajaran matematika yang ada di SMA maka untuk postingan kali ini dihadirkan materi lanjutan mengenai sistem pertidaksamaan linear dua variabel. Pada materi di bawah ini akan dijabarkan mengenai pengertian, contoh soal, Serta pembahasan tentang sistem pertidaksamaan dua variabel. So, perhatikan dengan baik penjelasan materi matematika berikut ini:

Pertidaksamaan linear dapat diartikan sebagai sebuah pertidaksamaan dimana peubah bebasnya memiliki bentuk linear (berpangkat satu). coba kalian ingat lagi bentuk-bentuk pertidaksamaan berikut ini:

3x = 6 (pertidaksamaan linear dengan satu peubah)

2x + y < 0 (Pertidaksamaan linear dengan dua peubah)

2x + 3y - 4z >0 (Pertidaksamaan linear dengan tiga peubah)

Pda postingan ini saya akan membatasi penjelasan hanya pada pertidaksamaan linear dua peubah. Gabungan dari dua atau lebih pertidaksamaan linear dengan dua peubah dapat disebut sebagai pertidaksamaan linear dua variabel. Contoh dari sistem persamaan linear dua variabel adalah:

2x + 4y ≥ 16

x + y ≥ 8

x ≥ 0

y ≥ 0

Himpunan dan Daerah Penyelesaian Pertidaksamaan Linear Dua Variabel

Berikut ini adalah cara yang dapat dilakukan untuk menentukan himpunan ataupun daerah penyelesaian dari sistem pertidaksamaan dua variabel: ax + by ≤  c

Pertama, buatlah garis ax + by = c dengan cara menentukan dua titik yang berbeda pada garis tersebut di dalam diagram cartesius. Diagram kartesius nantinya akan terbagi menjadi dua bagian yang dipisahkan oleh garis itu.

Kedua, Lakukan subtitusi terhadap sebuah titik pada salah satu bagian ke dalam sistem pertidaksamaan tersebut. Jikalau hasilnya merupakan pernyataan yang benar, artinya daerah tersebut merupakan penyelesaiannya, akan tetapi bila pernyataanya salah maka bagian lain lah yang menjadi penyelesaiaanya.

Ketiga, arsirlah pada bagian yang menjadi daerah penyelesaian.

Untuk lebih jelasnya, perhatikan contoh soal berikut ini:

Contoh Soal 1

Coba tentukanlah daerah penyelesaian yang memenuhi sistem pertidaksamaan 2x + 3y ≤ 12

Jawab :

Gambar garis 2x + 3y ≤ 12, pilih dua titik

Apabila x = 0 maka :

2.0 + 3y = 12

3y = 12 

y = 4 titik (0,4)

Apabila y = 0 maka:

2x + 3.0 = 12

2x = 12 

x = 6 titik (6,0)

Pertama, pilihlah titik (0,0) kemudian subtitusikan titik tersebut ke dalam pertidaksamaan 2x + 3y ≤ 12. dari perhitungan di atas diketahui hasilnya adalah 2 x 0 + 3 x 0 ≤ 12 atau 0≤ 12 sehingga pernyataannya bisa dianggap benar. Sehingga dapat disimpulkan bahwa daerah penyelesaian dari pertidaksamaan tersebut berada pada daerah yang ada di bawah garis sampai kepada garis yang menjadi batas 2x + 3y = 12. Sehingga gambarnya menjadi:

Untuk kali ini cukup sekian dulu materi tentang Sistem Pertidaksamaan Linear Dua Variabel Kelas X SMA. Pada postingan selanjutnya mungkin akan dibahas lebih lanjut mengenai materi-materi yang berkaitan dengan system pertidaksamaan linear dua variable. Oleh sebab itu, ikuti terus materi pelajaran matematika yang diposting di dalam blog ini agar kalian tidak ketinggalan untuk bisa mempelajari beragam pembahasan materi matematika yang ada di blog ini.

Contoh Soal Try Out Matematika SMP Ujian Nasional Kelas 9

Contoh Soal Try Out Matematika SMP - Alhamdulillah, pada akhirnya Rumus Matematika Dasar dapat memberikan sebuah artikel yang berisi contoh soal ujian nasional untuk siswa SMP kelas 9. Semoga contoh soal try out yang diberikan di bawah ini mampu membantu kalian semua yang duduk di bangku SMP kelas 9 sebagai sarana latihan dalam rangka menghadapi ujian nasional. Soal ini berisikan beragam materi mulai dari faktorisasi aljabar, sampai materi mengenai himpunan. Harapannya adalah agar contoh soal ini bisa kalian gunakan untuk belajar dan mempersiapkan diri sebelum melaksanakan UN sehingga dapat memperoleh nilai yang memuaskan. Yuk mari langsung saja kita lihat contoh soal try out matematika berikut ini:

Contoh Soal Try Out Ujian Nasional Matematika SMP

Soal 1

Hasil  penjumlahan dari 5x + 3y - 4 dengan x - 5y - 1 adalah...

a. 6x - 2y - 5

b. 6x - 8y - 5

c. 6x - 2y + 4

d. 6x - 2y + 5

Soal 2

Bentuk faktor dari 6x² - 7x - 10 adalah ...

a. (x - 2)(6x + 5)

b. (x + 2)(6x - 5)

c. (2x - 5)(3x + 2)

d. (2x + 5)(3x - 2)

Soal 3

Hasil dari (5x - 7)(2x + 4) adalah ...

a. 10x²- 34x - 28

b. 10x²+ 34x - 28

c. 10x²- 6x - 28

d. 10x²+ 6x - 28

Soal 4

Hasil dari     3     +    5     adalah ...

                x + 5      x - 3

a.    8x + 16__

   (x + 5)(x - 3)

b.    5x + 16__

   (x + 5)(x - 3)

c.    3x – 16__

   (x + 5)(x - 3)

d.     8x + 8 ­­­­­­­­­­­__

   (x + 5)(x - 3)

Soal 5

Bentuk paling sederhana dari 2x² + 15 - 27 adalah ...

                                                  4x² - 9

a.   x – 9_

    2x - 3

b.   x + 9_

    2x + 3

c.   x + 3_

    2x + 1

d.   x + 3_

    2x + 3

Soal 6

Bentuk sederhana dari          3         -            2_      adalah …

                                      x2 + x - 2      x2 + 3x + 2

a.            x + 5_____

   (x + 2)(x + 1)(x -1)

b.            x + 1_____

   (x + 2)(x + 1)(x -1)

c.             x – 5_____

   (x + 2)(x + 1)(x -1)

d.              x – 1____

   (x + 2)(x + 1)(x -1)

Soal 7

Diagram panah untuk relasi faktor dari dari A = {2, 3, 5, 7} ke B = {6, 9, 10} adalah ...

Soal 8

(i).{(3,2),(4,3),(5,4),(6,5)}

(ii).{(6,1),(7,2),(8,1),(6,3)}

(iii).{(8,a),(6,b),(8,c),(4,d)}

(iv).{(p,q),(q,r),(p,s),(t,s)}

Himpunan pasangan berututan di atas yang merupakan fungsi adalah ...

a. (i)

b. (ii)

c. (iii)

d. (iv)

Semoga Contoh Soal Try Out Matematika SMP Ujian Nasional Kelas 9 yang sudah di-share di atas, bisa bermanfaat bagi adik-adik sekalian. Semoga sukses dan mampu menjawab soal-soal matematika di dalam ujian nasional dengan baik.

5 Contoh Soal Cerita Aljabar Matematika

Contoh Soal Cerita Aljabar Matematika - Materi pelajaran matematika mengenai aljabar bisa dibilang gampang-gampang susah. Jika kalian sudah memahami setiap konsep dan sifat aljabar tentu akan mudah dalam mengerjakan soal-soalnya. Akan tetapi untuk kalian yang belum memahami pengertian aljabar, tentu akan sulit dalam mengerjakannya. Ya, mempelajari meteri ini memang membutuhkan konsentrasi dan kecermatan dalam menghafalkan pola-pola perhitungan di dalam aljabar.

Nah, untuk melatih kemampuan kalian di dalam megerjakan soal-soal yang berkaitan dengan materi matematika mengenai aljabar, tidak ada salahnya apabila kalian mencoba untuk menyelesaikan soal-soal yang diberikan oleh Rumus Matematika Dasar di bawah ini. Soal ini agak berbeda kerena disajikan dalam bentuk soal cerita sehingga kalian harus memperhatikan dengan baik setiap simbol dan angka-angka yang terdapat di dalam soal tersebut agar nantinya kalian tidak melakukan kesalahan di dalam menjawab soal-soal tersebut.

Kumpulan Contoh Latihan  Soal Cerita  Matematika Mengenai Aljabar

Soal 1

Diketahui panjang dari sebuah persegi panjang adalah (2x - 5) cm sedangkan lebarnya adalah (3x + 1), Maka tentukanlah:

a. Keliling persegi panjang yang dinyatakan dalam x

b. ukuran persegi panjang apabila diketahui kelilingnya adalah 23 cm

Soal 2

Lima tahun yang lalu, usia seorang ibu beserta kedua anak kembarnya adalah 40 tahun. Apabila pada saat itu usia sang ibu adalah 30 tahun, Maka berapakah umur dari masing-masing anak kembarnya saat ini?

Soal 3

Pak Budi melakukan sebuah perjalanan keluar kota. awalnya ia mengendarai motor selama 3 jam dengan kecepatan rata-rata (2x - 5)km/jam. Setelah itu pak ketut melanjutkan perjalanan dengan menaiki bus selama 4 jam dengan kecepatan rata-rata (5x + 8) km/jam. Maka tentukanlah:

a. Jarak yang ditempuh dalam x

b. nilai x apabila jarak yang ditempuh adalah 329km

Soal 4

Sebuah model kerangka balok dibuat dari kawat dengan ukuran panjang (2x - 3) cm, lebar (3x + 10) cm dan tinggi x cm. tentukanlah:

a. Panjang kawat dalam x

b. nilai x jika panjang kawat adalah 388cm

c. ukuran kerangka balok

Soal 5

Di sebuah meja terdapat 5 sendok, 5 piring, dan 5 gelas. Budi mengambil 1 buah sendok dan piring. Lalu Ani menaruh 2 buah piring, 3 sendok, dan 1 gelas. Maka berapakah jumlah peralatan makan yang tersedia di meja tersebut sekarang?

Itulah 5 buah Contoh Soal Cerita Aljabar Matematikayang bisa kalian manfaatkan untuk melatih diri dalam memahami bagaimana cara menggunakan konsep-konsep aljabar di dalam menjawab soal. Semoga bisa membuat kalian semakin paham dan mahir dengan materi mengenai aljabar yang diberikan dan diajarkan oleh guru kalian di sekilah.

Pengertian Sifat Komutatif Matematika, Contoh Soal dan Pembahasan Lengkap

Pengertian Sifat Komutatif Matematika - Selain sifat distributif yang sudah dijelaskan sebelumnya, di dalam matematika juga ada yang dinamakan dengan sifat komutatif. Tahukah kalian apa yang dimaksud dengan sifat komutatif matematika? jika belum tahu, Di sini Rumus Matematika Dasar akan menjelaskannya untuk kalian. Secara sederhana, sifat komutatif dapat kita artikan sebagai sifat pertukaran di dalam operasi hitung matematika, coba perhatikan perhitungan pada gambar di bawah ini:

Jadi bisa disimpulkan bahwa sifat komutatif di dalam matematika memenuhi rumus a + b = b + a dimana a dan b adalah bilangan bulat. Sifat tersebut tidak hanya berlaku pada operasi penjumlahan namun juga berlaku untuk operasi perkalian (a x b = b x a). Jadi, di  sifat komutatif matematika kita diperbolehkan melakukan pertukaran angka di dalam penjumlahan dan perkalian dengan hasil yang tetap sama.

Pengertian Sifat Komutatif Matematika, Contoh Soal dan Pembahasan

Sifat komutatif pada operasi hitung penjumlahan

Sekarang mari kita pelajari lagi konsep sifat komutatif pada operasi hitung penjumlahan di bawah ini:

Contoh Soal 1

Hitunglah hasil dari 26.983 + 99.281 = ...

Jawab:

Hasil dari 26.983 + 99.281 = 126.264

Apabila kedua bilangan tersebut ditukar tempatnya, apakah hasilnya akan tetap sama?

99.281 + 26.983 = 126.264

Ternyata hasilnya tetap sama, yaitu 126.264. Artinya hukum komutatif berlaku untuk operasi hitung penjumlahan.

Sifat komutatif pada operasi hitung pengurangan

Sekarang mari kita coba dalam operasi hitung pengurangan.

99.281 - 26.983 = 72.298

Seandainya posisi bilangannya ditukar apakah hasilnya sama?

26.983 - 99.281 = - 72.298

Terlihat bahwa hasilnya berbeda, jika posisi bilangan itu ditukar maka hasilnya akan menjadi negatif. Artinya, sifat komutatif tidak berlaku untuk operasi hitung pengurangan (a – b ≠ b – a)

Sifat komutatif pada operasi hitung perkalian

Selanjutnya, mari kita lihat penggunaan sifat tersebut di dalam operasi hitung dalam bentuk perkalian. Amati contoh soal di bawah ini:

Contoh Soal 2

Berapakah hasil dari 25 x 45 = ...

Jawab:

Hasil dari 25 x 45 = 1125

Untuk menguji sifat komutatif, mari kita tukar posisinya:

45 x 25 = 1125

Ternyata hasilnya pun tetap sama, artinya di dalam operasi hitung bentuk perkalian, sifat komutatif matematika dapat berlaku.

Sifat komutatif pada operasi hitung pembagian

Sekarang mari kita lihat apakah sifat ini bisa berlaku untuk operasi hitung pembagian. Kita ambil contoh pembagian di bawah ini:

80 : 20 = 4

Apabila ditukar apakah hasilnya akan sama?

20 : 80 = 0,25

Ternyata setelah posisinya ditukar hasil yang didapatkan justru berbeda. Maka dapat disimpulkan bahwa sifat komutatif tidak bisa berlaku di dalam operasi hitung pembagian (a : b ≠ b : a)

Bagaimana? apakah kalian sudah paham dengan penjelasan materi seputar Pengertian Sifat Komutatif Matematika, Contoh Soal dan Pembahasan Lengkap yang sudah dijabarkan di atas? Kalau belum, coba kalian baca lagi dengan seksama, pasti kalian akan bisa memahaminya jika memperhatikan dengan baik contoh-contoh perhitungan yang diberikan.

Rumus Matematika Faktorisasi Suku Aljabar Kelas 8 SMP

Faktorisasi Suku Aljabar  - Pemfaktoran atau biasa disebut juga sebagai faktorisasi bentuk aljabar merupakan suatu cara yang digunakan untuk menyatakan bentuk aljabar yang semula berbentuk penjumlahan menjadi suatu bentuk yang lain (perkalian). Untuk memahami lebih jauh mengenai bagaimana cara melakukan faktorisasi terhadap berbagai macam bentuk aljabar, sebaiknya kalian mengamati dengan baik penjelasan rumus matematika dasar yang ada di bawah ini:

Penjelasan Materi Rumus Matematika Faktorisasi Suku Aljabar untuk SMP Kelas 8

1. Pemfaktoran Bentuk ax + ay + az + … dan ax + bx – cx

Untuk menyelesaikan aljabar dengan bentuk di atas, kalian bisa menggunakan sifat distributive sebagai berikut:

ax + ay + az + … = a (x + y + z + …)

ax + bx + cx = x (a + b + c)

Coba kalian amati contoh soal berikut ini:

Contoh Soal 1:

Tentukan faktorisasi dari bentuk aljabar berikut ini:

a. 2x + 2y

b. pq²r³ + 2p²qr + 3pqr

Cara Menjawab:

a. 2x + 2y = 2 (x + y)

b. pq²r³ + 2p²qr + 3pqr = pqr (qr² + 2p + 3)

Sekarang coba kalian kerjakan soal-soal di bawah ini:

1. 3x – 3y =

2. 2x + 6 =

3. 4x²y – 6xy² =

4. 8pq + 24pqr =

5. 15x²– 18xy + 9xz =

2. Pemfaktoran Bentuk Aljabar selisih dua kuadrat x² – y²

Untuk melakukan faktorisasi aljabar yang berbentuk selisih dua kuadrat dapat kita bisa menggunakan cara berikut:

x²– y²  = x² _{+ (xy – xy) - y}²

             = (x² + xy) – (xy + y²)

             = (x – y)(x + y)

Sekarang amatilah contoh soal berikut ini:

Contoh Soal 2

Tentukan Faktorisasi dari bentuk aljabar di bawah ini:

a. x² – 4

b. 9x² – 25y²

Cara Menjawabnya:

a. x² – 4 = x²– 2² = (x – 2)(x + 2)

b. 9x² – 25y²= 3² x² – 5² x² = (3x) ²– (5y) ² = (3x – 5y)(3x + 5y)

Coba selesaikan soal-soal latihan berikut:

1. x²– 25 =

2. 9m²– 16 =

3. 25p²– 16q² =

4. 36x²– 81y² =

5. 81p²– 100q² =

3. Pemfaktoran Aljabar Bentuk Kuadrat Sempurna

Selanjutnya, untuk aljabar dengan bentuk kuadrat sempurna, pola pemfaktorannya adalah sebagai berikut:

x² + 2xy + y² = (x + y)²

x²– 2xy + y² = (x – y)²

Contoh Soal 3

Tentukan faktor kuadrat sempurna dari x² + 4x + 8

Cara Menjawabnya:

Gunakan saja sifat distributif -> 4x = 2x + 2x maka:

x²+ 4x + 8 = x² + 2x + 2x + 4

            = (x² + 2x) + (2x + 8)

            = x (x + 2) + 2(x + 2)

            = (x + 2) (x + 2)

            = (x + 2)²

Untuk kali ini sekian dulu materi Rumus Matematika Faktorisasi Suku Aljabar Kelas 8 SMP untuk lebih lengkapnya bisa kalian lihat pada materi lanjutan mengenai Pemfaktoran Bentuk Aljabar Kelas 8 SMP semoga kalian bisa memahami pembahasan di atas dengan baik.